题目链接
2019牛客多校第二场
background
出题人:sd0061
赵轩昂,北京航空航天大学,WorldFinal 2015/2016
Eddy
好像就是出题人的电脑用户名
出题评价
题目对我这个菜鸡来说较难,题意复杂
讲题评价
逻辑清晰,对每一题的讲解由浅入深,对时间复杂度不断优化精细讲解,层层入深,获得大家的一致好评(只是目前我这个菜鸡对于很多浅的地方还没学好甚至还没学过,所以补补补o(╥﹏╥)o)
A
题意
- Eddy大佬走路
先让0->N-1都有标记 -> 第i天走一圈需要Ni步(每天脚长不一样还行),可以前进和后退,然后收集完所有标记(每个地方都有标记,即0->N-1处都是标记)就立马感到无聊了就立马回去吃饭睡觉打豆豆(你的记录值中Eddy大佬走到Mi就算是收集完了所有的标记)
- 你每天观摩大佬走路(giao)
- 你复查数据的时候,你不确定到底数据是不是对的,然后你想知道这些天的数据正确的可能性(所以很自然的知道后面为什么要你输出前缀积,原来写笔记确实可以加深理解奥)
- T组测试(T天的观测)
- 然后每组测试都是给你Ni和Mi(每天Eddy的走路信息)
Output
- 输出前i天的数据都正确的可能性(也就是每天可能性之积)
思路
- Corner Case:
- 当N=1的时候,也就是1步就可以走完一圈,无论Eddy大佬前进还是后退,肯定是1步走完(这样肯定收集完了所有的标记),所以可能性为1
- 当M=0的时候,你记录的是Eddy大佬在0处就收集完了所有的标记,这是不可能,因为Eddy大佬一开始从0出发,所以一开始就已经拥有0号标记了,而一旦Eddy收集完所有的标记之后必定会立马回家,所以离开的地方的那个标记一定是最后收集到的,而且是第一次收集到的那个标记,所以你记录值为0显然是错的,所以可能性是0
- 一般情况(N非1,M非0)
- 有了上面M=0的理解,这里就好理解了,因为Eddy大佬一开始从0出发,然后Eddy大佬可以前进也可以后退,所以Eddy大佬最后一个到达的点可以是非0的其他任意一个点,所以最后到达每个点的可能性都是等概的,也就是
1/(N-1)
- 对了,输出的是前i的概率积
AC代码(自己再手写一遍收获更多)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
| #include<bits/stdc++.h>
using namespace std;
#define ll long long
const int mod = 1e9+7;
int T,n,m;
ll ans;
ll mul(ll a,ll b){
a *= b;
return a>=mod?a%mod:a;
}
ll qpow(ll a,ll b){
ll ret = 1;
while(b){
if(b&1) ret = mul(a,ret);
b>>=1;
a = mul(a,a);
}
return ret;
}
ll inv(ll a){ return qpow(a,mod-2); }
ll solve(ll n,ll m){
if(n==1) return 1;
if(m==0) return 0;
return inv(n-1);
}
int main(){
ios::sync_with_stdio(false);
ans = 1;
cin>>T;
while(T--){
cin>>n>>m;
ans = mul(ans,solve(n,m));
cout<<ans<<endl;
}
return 0;
}
|
B
emmmm,看懂了一点点题解,但是对于题解中的BM完全不熟悉,所以先留坑
C,D自己太菜了,留坑
E
emmmm,看懂了一点点题解,但是还是不太熟悉基础的算法,我先去补基础的算法,留坑
F
题意
给定2N个人,(N <= 14),两两间有边权,把这2N个人分为2组,每组N个,求两组间的边权和最大
题解
朴素法(也称暴力法),在新加入一个人的时候,比如说加入了A组,那么直接将它与B组间已经有的所有人的边权加一遍
AC代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
| #include<bits/stdc++.h>
using namespace std;
#define ll long long
const int M = 50;
int d[M][M];
int a[M],b[M];
int cnt1,cnt2;
ll ans;int N;
void dfs(int cur,ll val){
if(cur>2*N){ ans = max(ans,val);return ;}
if(cnt1<N){
a[cnt1++]=cur;
ll tmp = 0;
for(int i=0;i<cnt2;i++) tmp+=d[cur][b[i]];
dfs(cur+1,val+tmp);
cnt1--;
}
if(cnt2<N){
b[cnt2++]=cur;
ll tmp = 0;
for(int i=0;i<cnt1;i++) tmp+=d[a[i]][cur];
dfs(cur+1,val+tmp);
cnt2--;
}
}
int main(){
ios::sync_with_stdio(false);
cin>>N;
for(int i=1;i<=2*N;i++)
for(int j=1;j<=2*N;j++)
cin>>d[i][j];
ans = 0;
dfs(1,0);
cout<<ans<<endl;
return 0;
}
|
G计算几何,留坑
H
题意
给定一个N*M的01矩阵(1<=N,M<=1000),求第二大全是1的矩阵面积
题解
- 枚举每一行,以当前行为底,记录每一列往上不间断最多延长多远,那么这样之后就变成了一维的柱状图求最大/次大/k大矩形面积,可用单调栈求解
- 由于要记录第二大,之前求最大的做法(poj2559)是直接用max维护ans,width合并的做法在这里就要改成把所有解先丢进一个vector(之后排序复杂度
ans个数 * log(ans个数))(或者维护一个k大的小值优先的priority_queue,复杂度算上维护也是ans个数 * log(ans个数))
- 但是这里必须把
(width-1)*ddz[top]也放入状态级,因为求第二大,所以只要把次大状态加入(详细原因看下面说的坑点)
- 所以推荐使用把全状态扔进vector,这样还可以求第k大,虽然慢点
坑点
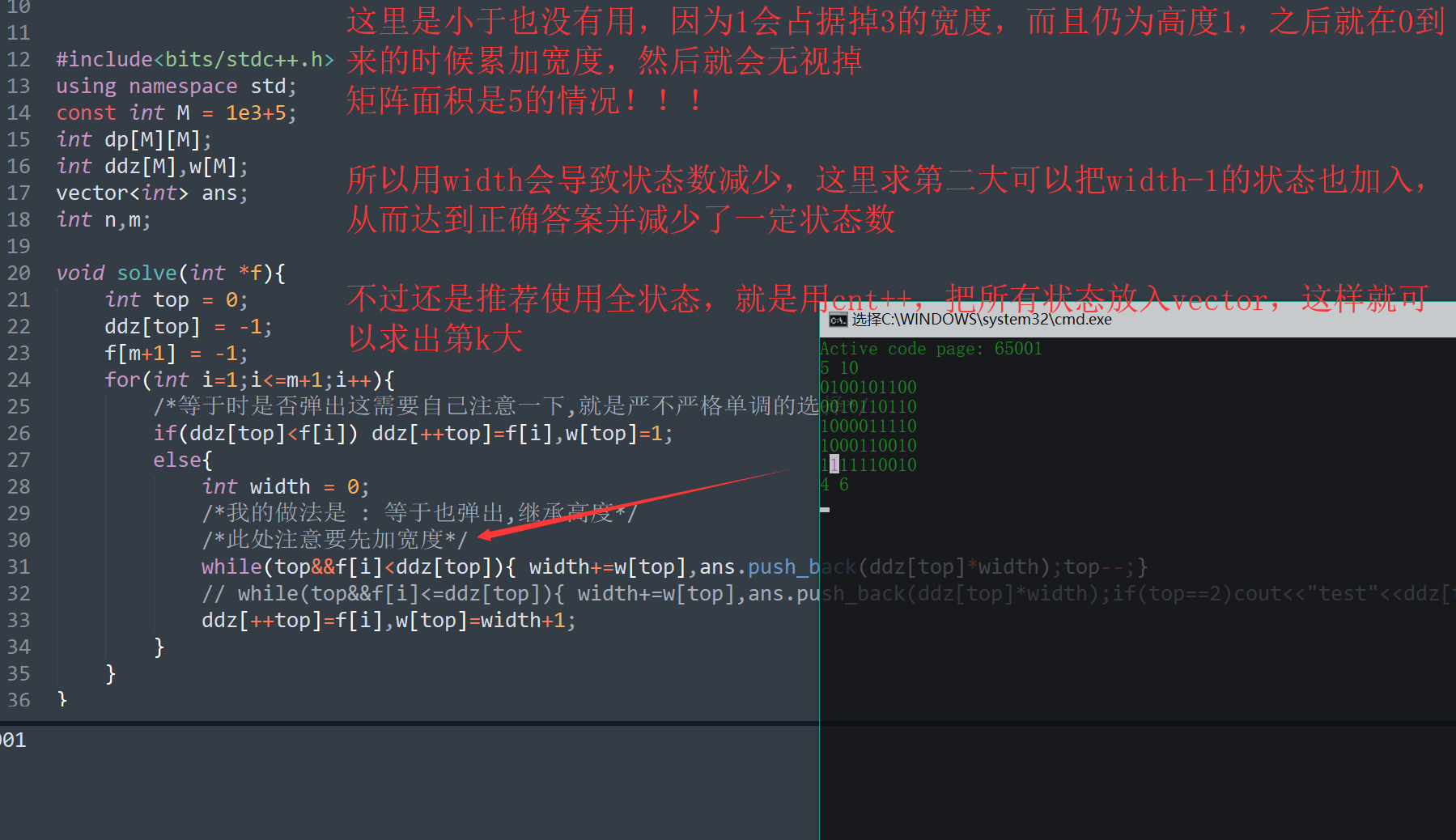
图中最后一行样例的dp的单调栈
这里是小于也没有用,因为1会占据掉3的宽度,而且仍为高度1,之后就在0到来的时候累加宽度 **(宽度直接从4加到了6,跳过了5,因为1之前会占据掉3的宽度)**,然后就会无视掉
矩阵面积是5的情况!!!
所以用width会导致状态数减少,这里求第二大可以把width-1的状态也加入,从而达到正确答案并减少了一定状态数
不过还是推荐使用全状态,就是用cnt++,把所有状态放入vector,这样就可以求出第k大
![]()
AC代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
|
#include<bits/stdc++.h>
using namespace std;
const int M = 1e3+5;
int dp[M][M];
int ddz[M],w[M];
vector<int> ans;
int n,m;
void solve(int *f){
int top = 0;
ddz[top] = -1;
f[m+1] = -1;
for(int i=1;i<=m+1;i++){
if(ddz[top]<f[i]) ddz[++top]=f[i],w[top]=1;
else{
int width = 0;
while(top&&f[i]<ddz[top]){ width+=w[top],ans.push_back(ddz[top]*width),ans.push_back(ddz[top]*(width-1));top--;}
ddz[++top]=f[i],w[top]=width+1;
}
}
}
int main(){
char c[M];
while(~scanf("%d%d",&n,&m)) {
ans.clear();
for(int i=1;i<=n;i++){
scanf("%s",c);
for(int j=1;j<=m;j++) dp[i][j] = c[j-1] == '0'? 0 : dp[i-1][j]+1;
}
for(int i=1;i<=n;i++) solve(dp[i]);
sort(ans.begin(),ans.end());
int sz = ans.size();
if(sz<=1) printf("0\n");
printf("%d\n", ans[sz-2]);
}
return 0;
}
|
I听Eddy大佬说有7种dp,太难留坑
J也太难留坑