CF589_C Primes and Multiplication tutorial 详解算法日常[31/100]

Linmin.Shan included in 算法学习日常

2019-09-30 549 words 2 minutes

Contents

题目链接

CF589_C Primes and Multiplication

题解

官方题解

题解解释

题解中的式子

$\begin{aligned} \prod_{i=1}^{n} f(x, i) &= \prod_{i=1}^{n} \prod_{p \in prime(x)} g(i, p) \ &= \prod_{i=1}^{n} \prod_{p \in prime(x)} p^{h(i,p)} \ &= \prod_{p \in prime(x)} \prod_{i=1}^{n} p^{h(i,p)} \ &= \prod_{p \in prime(x)} p^{\sum_{i=1}^{n} h(i, p)} \ &= \prod_{p \in prime(x)} p^{h(n!, p)} \end{aligned}$

算法优化式子的解释

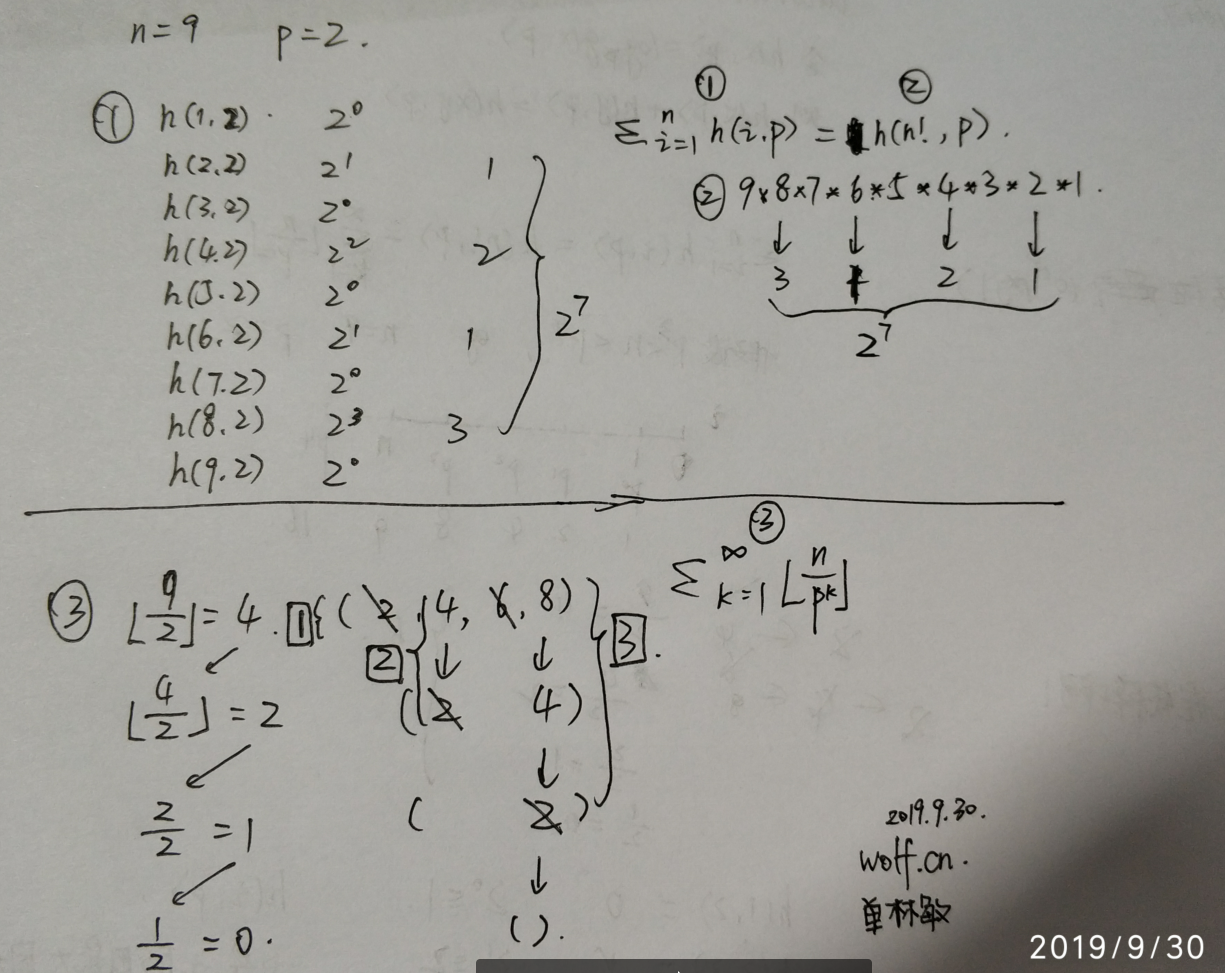
${\sum_{i=1}^{n} h(i, p)} = h(n!, p) = \sum_{k=1}^{\infty} \Bigl \lfloor \frac{n}{p^k} \Bigr \rfloor$

左边两项相当于1到n,各项找p的最大幂的因子(我们需要的是那个幂),大多数项是0次幂,即最大因子为1,其他的都是1到n中恰好为p的幂次,而且这个幂次只出现一次! –> 然后获取所有的幂次和

右边的式子则是让n值不断除p(记录第i次相除,i从1到 $\Bigl \lfloor \frac{n}{p} \Bigr \rfloor$ ),在第i次判断n内各个数的集合中的因子含有 $p^i$ 的数字个数,记录这些个数的和值

因为最终两个和值都是记录的1到n中所有数的p的因子出现次数,所以是相等的!(没看懂没有关系,看后面的例子体会一下)

h(i,p) 解释

p是素数,然后h(i,p)表示p的多少次方等于i
即 $p^{h(i,p)}$ = i

举例解释

假设n=9,p=2

AC代码

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36


#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
#define rep(i, a, b) for(int i = int(a); i <= int(b); ++i)
#define per(i, b, a) for(int i = int(b); i >= int(a); --i)
#define mem(x, y) memset(x, y, sizeof(x))
#define SZ(x) x.size()
#define mk make_pair
#define pb push_back
#define fi first
#define se second
const ll mod=1000000007;
const int inf = 0x3f3f3f3f;
inline int rd() {int x=0;char p=getchar();while(p<'0'||p>'9')p=getchar();while(p>='0'&&p<='9')x=x*10+p-'0',p=getchar();return x;}
inline ll qpow(ll a,ll b){ll ans=1%mod;for(;b;b>>=1){if(b&1)ans=ans*a%mod;a=a*a%mod;}return ans;}
ll x,n,ans=1;

ll f(ll p){
    ll m=n,sum=0;
    while(m) m/=p,sum+=m;
    return qpow(p,sum);
}

int main(){
    scanf("%lld%lld",&x,&n);
    for(int i=2;i*i<=x;i++){
        if(x%i==0){
            ans=ans*f(i)%mod;
            while(x%i==0) x/=i;
        }
    }
    if(x!=1) ans=ans*f(x)%mod;
    printf("%I64d\n",ans);

    return 0;
}

每天一句叨叨

哭过，痛苦过，但从没有放弃过。笑过，坚持过，因此不曾后悔过。