后缀数组基础题poj1743详解_算法日常[16/100]

发表于 更新于 分类于 阅读次数：
后缀数组基础题poj1743详解_算法日常 POJ1743 为什么c+1,ans+1 为什么da函数的n值要加1而getheight函数不用 height分组为什么直接遍历下去分就好，不用吧height值相同的放在一起

POJ1743

题目链接

POJ上面

VJ上面

题意

给定一个字符串，求最长重复子串，这两个子串不能重叠

解题思路

  • 由于配置不是简单的匹配，有升降调的处理，但是我们无法确定升降的幅度，所以我们首先对输入的数组进行差值处理
  • 可以发现同一个旋律的区段，它们的差值数组是相等的
  • 因为之前我们处理成了差值，所以我们内卷了一个值，我们的差值相当于左右两个值，所以4个值代表着5个值
  • 所以只要找到最长相同串长的长度不小于4的差值区段即可
  • 由于需要求出最长的长度，考虑二分后验证可行性，二分区段的长度x，对差值数组求一遍后缀数组，将最长公共前缀大于等于x的划分成一组，如果存在一组的sa差值大于等于x+1(详见下面的重点解释)，那么就表示x长度的差值数组能够被找到。二分结束即可得到答案。

没学后缀数组？

出门左转给你后缀数组学习合集

思路重点

为什么c+1,ans+1

二分检查的时候，最长公共前缀是x,sa差值却要大于x+1:

因为之前我们处理成了差值，所以我们内卷了一个值，我们的差值相当于左右两个值，所以4个值代表着5个值.所以最长公共字串只要在4的时候就相当于5,然后sa的差值还是要相间隔5才行==>这样真实的5个值也才是真的间隔5个值，所以同理答案也就是c+1(ans+1)

比如:

1
2
1 2 3 4 5 6 7 8 9 10
 1 1 1 1 ' 1 1 1 1

中间的'也是1，但是代表的5,6，所以如果从这里开始和前面的4个1构成相同串的话，然后就重叠了一个，所以必须从'后面1开始

我看了别的几个博主对于这题的分析没有谈及，这里，还有些代码没有考虑这里也能AC，说明数据都去卡时间了，没有卡下面这个特例:

1
2
9
1 2 3 4 5 6 7 8 9

为什么da函数的n值要加1而getheight函数不用

da要加一个位置的字符,让它比所有的字符都小，所以这个字符起始的后缀是其本身，其排名为0(rank[n]=0,sa[0]=n)
然而calheight却不要…因为calheight直接从rank值为1(rank为0的地方是添加的最小字符)的地方记到n，根本不会用到sa[0](排名为0的后缀)，重点还有for中用的是<=..所以只要使用n.

for(i=1;i<=n;i++) ::rank[sa[i]]=i;

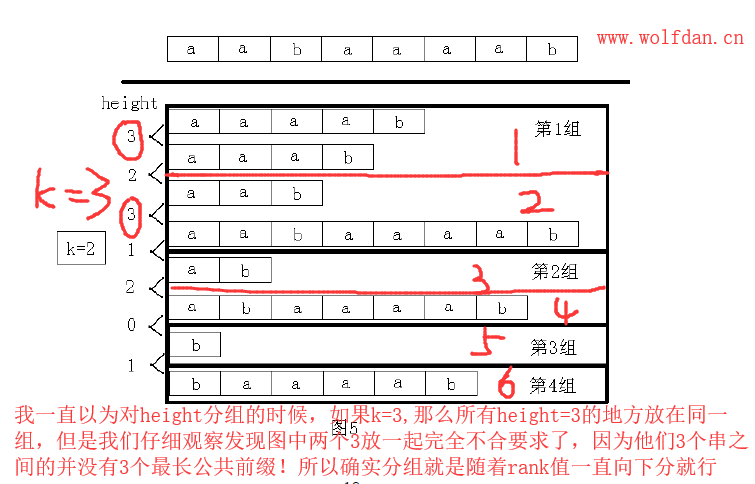
height分组为什么直接遍历下去分就好，不用吧height值相同的放在一起

AC代码1(推荐)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
#include<iostream>
#include<algorithm>
using namespace std;
typedef long long ll;
const ll mod=1000000007;
const int inf = 0x3f3f3f3f;
const int maxn = 20010;
int sa[maxn],rank[maxn],height[maxn];
int n;
int str[maxn];
int wa[maxn],wb[maxn],wv[maxn],ws[maxn];
int cmp(int *r,int a,int b,int l){return r[a]==r[b]&&r[a+l]==r[b+l];}

void da(int *r,int *sa,int n,int m){
    int i,j,p,*x=wa,*y=wb,*t;
    for(i=0;i<m;i++) ::ws[i]=0;
    for(i=0;i<n;i++) ::ws[x[i]=r[i]]++;
    for(i=1;i<m;i++) ::ws[i]+=::ws[i-1];
    for(i=n-1;i>=0;i--) sa[--::ws[x[i]]]=i;
    for(j=1,p=1;p<n;j*=2,m=p){
        for(p=0,i=n-j;i<n;i++) y[p++]=i;
        for(i=0;i<n;i++) if(sa[i]>=j) y[p++]=sa[i]-j;
        for(i=0;i<n;i++) wv[i]=x[y[i]];
        for(i=0;i<m;i++) ::ws[i]=0;
        for(i=0;i<n;i++) ::ws[wv[i]]++;
        for(i=1;i<m;i++) ::ws[i]+=::ws[i-1];
        for(i=n-1;i>=0;i--) sa[--::ws[wv[i]]]=y[i];
        for(t=x,x=y,y=t,p=1,x[sa[0]]=0,i=1;i<n;i++)
        x[sa[i]]=cmp(y,sa[i-1],sa[i],j)?p-1:p++;
    }
    return;
}

/*r为字符串数组,sa是后缀数组,n为字符串长度*/
void calheight(int *r,int *sa,int n){
    int i,j,k=0;
    /*用sa[]得到rank[]*/
    for(i=1;i<=n;i++) ::rank[sa[i]]=i;
    /*j就是后缀i的前一名的后缀位置,然后如果前一个串之间有k,那么就从k--起步*/
    for(i=0;i<n;height[::rank[i++]]=k)
    for(k?k--:0,j=sa[::rank[i]-1];r[i+k]==r[j+k];k++);
    return;
}

/*

为什么check里面的间隔是c+1:
    因为之前我们处理成了差值，所以我们内卷了一个值，
    我们的差值相当于左右两个值，所以4个值代表着5个值
    所以最长公共字串只要在4的时候就相当于5,然后sa的
    差值还是要相间隔5才行==>这样真实的5个值也才是真的
    间隔5个值，所以同理答案也就是c+1
*/
bool check(int c){
    int Max=sa[1],Min=sa[1];
    for(int i=2;i<=n;i++){
        /*这里的for是枚举的排名值，而height就是相邻排名的
        最长公共前缀,所以直接分组就行了*/
        if(height[i]>=c) Max=max(Max,sa[i]),Min=min(Min,sa[i]);
        else Max=sa[i],Min=sa[i];
        if(Max-Min>=c+1) return true;
    }
    return false;
}

int main(){
    ios::sync_with_stdio(false);cin.tie(0);
    while(cin>>n){
        if(n==0) break;
        for(int i=0;i<n;i++) cin>>str[i];
        for(int i=0;i<n-1;i++) str[i]=str[i+1]-str[i]+90;
        /*因为转变差值了，所以少一个值*/
        str[n-1]=0;n--;
        // for(int i=0;i<=n-1;i++) cout<<str[i]<<" "; cout<<endl;

        /*da要加一个位置的字符,让它比所有的字符都小
        然而calheight却不要...因为calheight直接从rank只为1(rank为0的地方是添加的最小字符)
        的地方记到n(用的是<=)..所以只要使用n.不需要n+1*/
        da(str,sa,n+1,178);
        calheight(str,sa,n);
        int l=0,r=n,ans=0;
        while(l<=r){
            int mid=(l+r)>>1;
            if(check(mid)) l=mid+1,ans=mid;
            else r=mid-1;
        }
        if(ans<4) cout<<0<<endl;
        else cout<<ans+1<<endl;
    }

    return 0;
}

AC代码2(RMQ版)

此AC代码为2019年8月22日做HDU5008(因为那题最好还是用RMQ的后缀数组题)的时候发现的
不过这题用RMQ比较鸡肋，为什么? 请看下面的代码头部注释

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
/*
今天在第二次研究hdu5008的时候,发现好多题目都是没有用rmq的
但是总有大佬不满足于暴力裸sa就完事,于是都加了rmq,
然后我有点看不懂,就去逛oi-wiki,发现居然有不重叠重复两次
的串也可以用rmq，那不就是我昨天做的poj1743的更优做法吗？
是的，然后就在网上搜到了O(test*(nlogn+logn))的做法！

之前的写法是O(test*nlogn)的

但是实测发现RMQ版的反而还慢了100多ms!好像是因为他的check还是O(n)而非O(1)的
因为这里的check是我们自己去寻找一个左右区间，而非输入直接给我们左右区间，
所以这里的寻找的复杂度是O(n),所以RMQ无济于补
而且RMQ是nlog(n)的预处理...  所以当然会慢啊 ---> 所以在更大一个量级的询问的时候再用比较好

----------------上面为简单分析-----下面为用途---------------
这里有rmq求排名区间内最远的sa位置差值
*/

#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
const int maxn=21000;
int dp1[maxn][20],dp2[maxn][20];
int mm[maxn];
int str[maxn],tmp[maxn];
int wa[maxn],wb[maxn],wv[maxn],ws[maxn];
int sa[maxn],ranks[maxn],height[maxn];
inline bool cmp(int *r,int a,int b,int l){
    return r[a]==r[b]&&r[a+l]==r[b+l];
}
void da(int *r,int n,int m){
    int i,j,p,*x=wa,*y=wb,*t;
    for(i=0;i<m;i++) ws[i]=0;
    for(i=0;i<n;i++) ws[x[i]=r[i]]++;
    for(i=1;i<m;i++) ws[i]+=ws[i-1];
    for(i=n-1;i>=0;i--) sa[--ws[x[i]]]=i;
    for(j=1,p=1;p<n;j*=2,m=p){
        for(p=0,i=n-j;i<n;i++) y[p++]=i;
        for(i=0;i<n;i++) if(sa[i]>=j) y[p++]=sa[i]-j;
        for(i=0;i<n;i++) wv[i]=x[y[i]];
        for(i=0;i<m;i++) ws[i]=0;
        for(i=0;i<n;i++) ws[wv[i]]++;
        for(i=1;i<m;i++) ws[i]+=ws[i-1];
        for(i=n-1;i>=0;i--) sa[--ws[wv[i]]]=y[i];
        for(t=x,x=y,y=t,p=1,x[sa[0]]=0,i=1;i<n;i++)
            x[sa[i]]=cmp(y,sa[i-1],sa[i],j)?p-1:p++;
    }
    for(i=0;i<n;i++) ranks[sa[i]]=i;
    int k=0;
    for(i=0;i<n-1;i++){
        if(k) k--;
        j=sa[ranks[i]-1];
        while(r[i+k]==r[j+k]) k++;
        height[ranks[i]]=k;
    }
    return;
}
void initRMQ(int n){
    /*mm其实是log,这里赋值为-1是为了后面mm[1]=0,也就是2^0=1*/
    mm[0]=-1;
    for(int i=1;i<=n;i++){
        /*(i&(i-1))==0表示n==0或者是2的倍数*/
        mm[i]=((i&(i-1))==0)?mm[i-1]+1:mm[i-1];
        /*这里是预处理sa的rmq*/
        dp1[i][0]=dp2[i][0]=sa[i];
    }
    for(int j=1;j<=mm[n];j++)
        for(int i=1;i+(1<<j)-1<=n;i++){
            dp1[i][j]=max(dp1[i][j-1],dp1[i+(1<<(j-1))][j-1]);
            dp2[i][j]=min(dp2[i][j-1],dp2[i+(1<<(j-1))][j-1]);
        }
}

int rmq(int x,int y){
    int k=mm[y-x+1];
    return max(dp1[x][k],dp1[y-(1<<k)+1][k])-min(dp2[x][k],dp2[y-(1<<k)+1][k]);
}

bool check(int len,int N){
    int s=1,e=1;
    while(e<N){
        if(height[e+1]>=len-1) e++;
        else{
            if(rmq(s,e)>=len) return true;
            s=++e;
        }
    }
    return false;
}

int main(){
    int N;
    while(scanf("%d",&N)&&N){
        for(int i=0;i<N;i++)
            scanf("%d",&str[i]);
        for(int i=0;i<N-1;i++)
            tmp[i]=str[i+1]-str[i]+90;
        tmp[N-1]=0;
        /*这里没有N--,所以直接使用的N,而RMQ使用的N-1,height封锁掉N号位置*/
        da(tmp,N,200);
        initRMQ(N-1);
        height[N]=-1;
        int left=1,right=N/2;
        while(left<=right){
            int mid=(left+right)/2;
            if(check(mid,N)) left=mid+1;
            else right=mid-1;
        }
        if(right<5) printf("0\n");
        else printf("%d\n",right);
    }
    return 0;
}

每天一句叨叨

我不管你是什么垃圾，我只看结果

要达到结果，你应该知道怎么做

I know you have the urge to give up!

But you must keep faith!

You do make a difference!